Cylindrical Reformulation of Heegaard Floer Homology

This page is about the cylindrical reformulation by Robert Lipshitz. The main references are Lipshitz Paper, errata, and lecture notes in Heegaard Floer Homology.

Generic Pointed Heegaard Diagram and Intersection Points

Let $\mathcal{H}$ be a pointed generic Heegaard Diagram.

Comment

The original two authors did not use the generic Heegaard diagram in the original formulation, but I guess we need this generic condition to evade the vacuously true in definition of admissible criterion.

Let denote $\alpha ={\alpha }_1\cup \cdots {\alpha }_g\subset {\Sigma }_g$ ,and similarly define $\beta ={\beta }_1\cup \cdots {\beta }_g\subset {\Sigma }_g$.

Domain

The curves $\alpha \cup \beta$ divide $\Sigma$ into a collection of path-connected components as ${\bigcup }_{k=1}^n\text{int}(D_k).$ The closed sets $D_k=D_k^o$ are called the elementary domains.
A domain $D={\sum }_{k=1}^n{n}_k{D}_k$ where $n_k$ is the algebraic multiplicity of the elementary domain $D_k$.

Remark

We can also see the domain $D$ as a formal sum of the homology class in $H_2({\Sigma }_g,\alpha \cup \beta )$.

Multiplicity of a domain

The multiplicity of the domain $D$ at $p\in \Sigma \setminus \alpha \cup \beta$, denoted as $n_p(D)$, is the coefficient of the elementary domain containing $p$ in the expression for $D$.

Intersection Point (Heegaard State)

An intersection point $\vec{x}$ is a $g$-tuple $\left\{x_1,\dots ,x_g\right\}$ where $x_i$‘s lie on ${\alpha }_i\cap {\beta }_{\sigma (i)}$. In the book, authors defined as Heegaard State.

Remark

A ${\text{Spin}}^{\mathbb{C}}(Y)$ structure $\mathfrak{s}$ depends on the choice of base point.

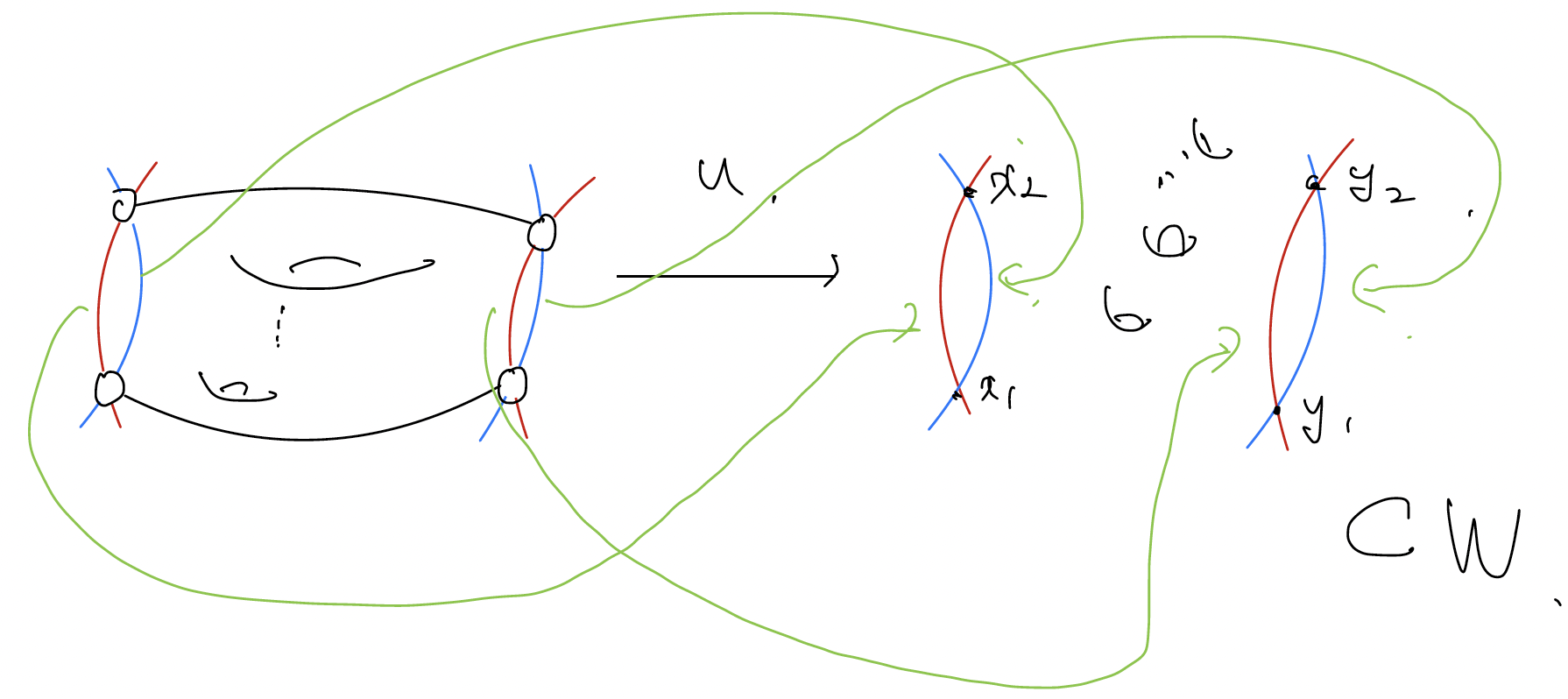
Cylindrical Construction

From now on I will assume $g\ge 2$ and drop $g$ in ${\Sigma }_g$ as $\Sigma$.
It is defined on $g\ge 2$ by a technical issue.
Since we can stabilize the genus $1$ Heegaard diagram, the formulation can hold for the $3$-manifolds.

Let $W=\Sigma \times [0,1]\times \mathbb{R}$, and denote $\mathbb{D}=[0,1]\times \mathbb{R}$.
The projection maps ${\pi }_{\Sigma }$, ${\pi }_{\mathbb{D}}$, and ${\pi }_{\mathbb{R}}$ are projection maps to the subscript component.
Also, let the Lagrangian cylinders $C_{\alpha }=\alpha \times \{1\}\times \mathbb{R}$ and $C_{\beta }=\beta \times \{0\}\times \mathbb{R}$.

We are going to count the holomorphic representative which has boundaries in $C_{\alpha }\cup C_{\beta }$.

Complex Structure

Let the Heegaard surface $\Sigma$ have a complex structure $j_{\Sigma }$ and area form $dA$.
Let the split symplectic form $\omega =dA+ds\wedge dt$ on $W$.
Let $J$ be an almost complex structure on $W$ as follows:

1. $J$ is tamed with $\omega$. It guarantees the compactness of the moduli space.
2. $J$ in a neighborhood of points ${\mathfrak{z}}_i$ splits as $j_{\Sigma }\times j_{\mathbb{D}}$.
3. $J$ is translation invariant in the $\mathbb{R}$-factor.
4. Cauchy-Riemann equation $\frac{\partial }{\partial s}=J\frac{\partial }{\partial t}$.
5. $J$ preserves $T(\Sigma \times \{s,t\})\subset TW$ for all $(s,t)\in I\times \mathbb{R}$.

The conditions 3 and 4 make $W$ a cylindrical setting.

Characteristic Foliation

Through the symplectic form $\omega$, for each $t\in \mathbb{R}$, we have a characteristic foliation
$\{p\}\times I\times \{t\}.$

Proof of it The kernel of $\omega$ restricted to $\Sigma \times I\times t=\left\{X\in T\Sigma :i_{X}dA=0\right\}$, equivalently, it is the set of $X$ satisfiying $dA(X,-)\equiv 0$ for each $(p,s)$. Since $X=v_p+a{\partial }_s$ and $dA$ is an area form that non-degenerate, $v_p=0$. Therefore $X=a{\partial }_S$.

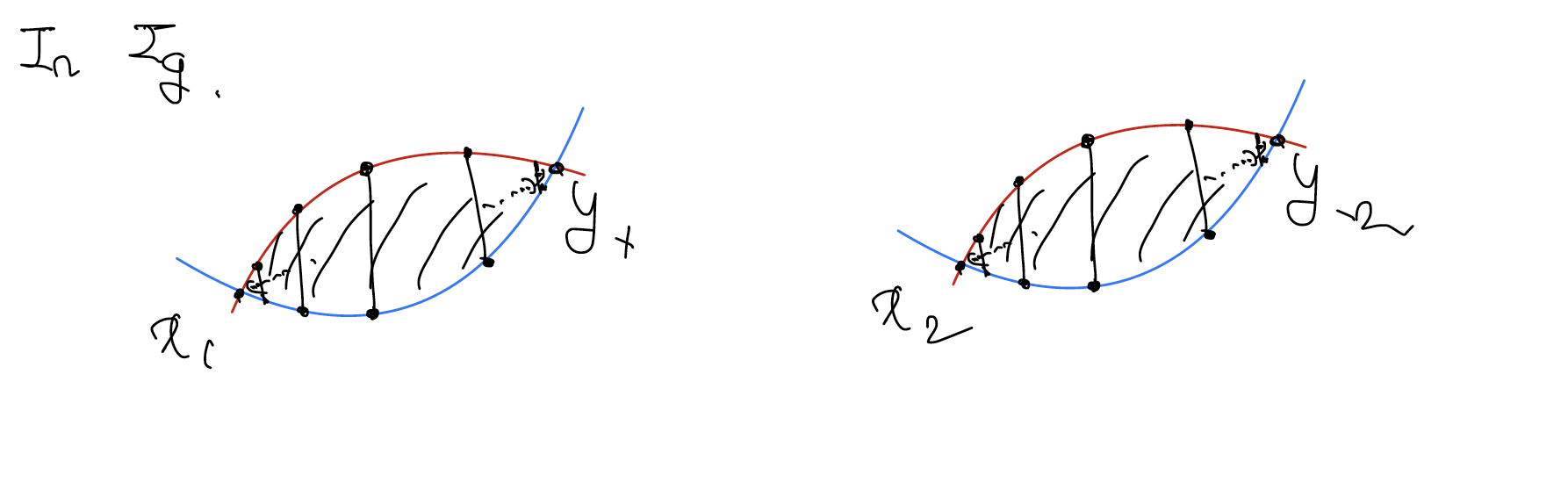
Let $\vec{x}$ be an intersection point.
Since we have a characteristic foliation, we have Reeb chords $\{x_i\}\times I$.

I-chord collection

A $g$-tuple of Reeb chords at $\pm \infty$ specified by an intersection point is called an I-chord collection.

We can compactify $W$ as $\overline{W}=\Sigma \times [0,1]\times [-1,1]$, and let $\overline{C_{\alpha }}$ and $\overline{C_{\beta }}$ be the closures.

---

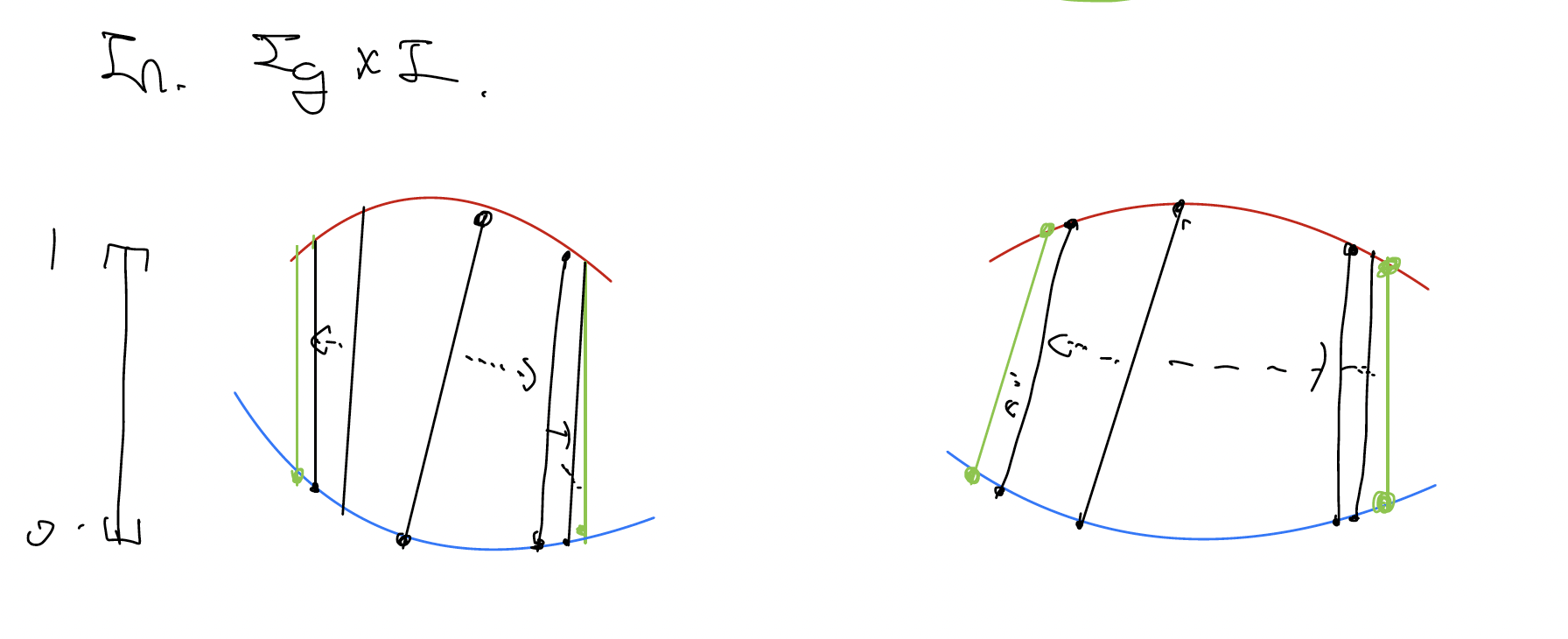
Holomorphic Curve and Connecting Domain

Let $S$ be a Riemann surface with boundary, with $g$ positive punctures $\{p_1,\dots ,p_g\}$ and negative punctures $\{q_1,\dots ,q_g\}$.
$S$ does not need to be connected and is compact away from the boundaries.

Holomorphic Curve Conditions

Let $u:(S,\partial S)\to W$ be $J$-holomorphic, satisfying:

1. $S$ is smooth.
2. $u$ is an embedding.
3. $u(\partial S)\subset C_{\alpha }\cup C_{\beta }$.
4. No component has constant ${\pi }_{\mathbb{R}}\circ u$.
5. Energy of $u$ is finite.
6. ${\lim }_{w\to p_i}{\pi }_{\mathbb{R}}\circ u(w)=+\infty$, ${\lim }_{w\to q_i}{\pi }_{\mathbb{R}}\circ u(w)=-\infty$.
7. For each $i$, $u^{-1}({\alpha }_i\times 1\times \mathbb{R})$ and $u^{-1}({\beta }_i\times 0\times \mathbb{R})$ each consist of exactly one component of $\partial S\setminus \{p_1,\dots ,q_g\}$.

Comment

I am not sure about the terminology “shadow”. My first thought was projection ${\pi }_{\Sigma }$, but professor pointed out holomorphicity of the projection map.

Connects between two I-chord collections

A holomorphic curve converges to an I-chord collection $\vec{x}$ near $-\infty$ and $\vec{y}$ near $+\infty$.
Denote ${\pi }_2(\vec{x},\vec{y})$ as the set of homology classes of $u$ connecting from $\vec{x}$ to $\vec{y}$.

Two homology classes $A$ and $B$ are equivalent if they are the same in
$H_2(\overline{W},\overline{C_{\alpha }}\cup \overline{C_{\beta }}\cup \{x_i\}\times [0,1]\times \{-1\}\cup \{y_i\}\times [0,1]\times \{1\}).$

Concatenation: If $A\in {\pi }_2(x,y)$ and $B\in {\pi }_2(y,z)$, then $A+B\in {\pi }_2(x,z)$.

Positive homology class

$A\in {\pi }_2(\vec{x},\vec{y})$ is positive if $n_{z_i}(A)\ge 0$ for all $i$.

Hat Pi 2

${\hat{\pi }}_2(\vec{x},\vec{y})=\{A\in {\pi }_2(\vec{x},\vec{y}):n_{\mathfrak{z}}(A)=0\}$.
Elements in ${\hat{\pi }}_2(\vec{x},\vec{x})$ are periodic classes.

Positivity of Domains

If $A\in {\pi }_2(\vec{x},\vec{y})$ has a holomorphic representative, then $n_{z_i}(A)\ge 0$.
The contraposition is useful to define the boundary map.

Moduli Space of the Domain

Moduli Space

Let $D$ be a domain of homology class $A\in {\pi }_2(\vec{x},\vec{y})$.
${\mathcal{M}}^A$ is the space of holomorphic curves connecting $\vec{x}$ and $\vec{y}$ in class $A$.
In the cylindrical setting, $\widehat{{\mathcal{M}}^A}={\mathcal{M}}^A/\mathbb{R}$, and $\overline{\widehat{{\mathcal{M}}^A}}$ its compactification.

Maslov Index Computation

The selling point of the paper, in my opinion, is “we can compute Maslov index combinatorially!“. Cylindrical Formulation for Heegaard Floer Homology. ¹

Admissibility

We need to ensure that the sum in the differential $\hat{\partial }$ runs over finitely many positive domains
$A\in {\pi }_2(x,y)$.
Admissible Criterion in Heegaard Floer Homology

Chain Complex of Heegaard Floer Homology

Example Computation of hat version of Heegaard Floer Homology

---

Footnotes

1. In Lipshitz’s paper has gaps in the proof. So, please check the errata. ↩